Optimisation sans contrainte d'une fonction de 2 variables
Deux variables ? D’accord, alors par esprit de contradiction commençons par faire du hors sujet.
Optimisation d’une fonction d’une seule variable
Une optimisation se traduit par la recherche d’un extremum global ou local d’une fonction. On s’adonne à ce sympathique exercice dès la classe de première. Ce ou ces points sont découverts en annulant la dérivée. Il reste ensuite à déterminer la nature de l’extremum : maximum ou minimum ? Les techniques habituellement employées au lycée sont le tableau de variation et la position de la tangente par rapport à la courbe représentative. Ajoutons une autre technique, celle de l’étude du signe de la dérivée seconde qui est plus « universelle », du moins si la fonction est deux fois dérivable.
En principe, le terme « optimisation » s’emploie lorsque l’étude de l’extremum s’inscrit dans le cadre d’applications plus ou moins concrètes. Sur ce site, vous pouvez notamment en trouver sur les pages application du théorème de la bijection ou coût marginal...
Optimisation d’une fonction de deux variables
Nous y voilà. Nombreux sont les phénomènes modélisables par une fonction de deux variables, définie sur un ouvert de \(\mathbb{R}^2.\) La recherche d’un extremum réclame des outils plus élaborés que si la variable vit seule mais la démarche reste la même : recherche du ou des points où s’annulent les deux dérivées partielles (qui se nomment les points critiques) puis détermination de leur nature à l’aide de la matrice hessienne : maximum, minimum ou point selle.
Matrice hessienne :
\(H = \left( {\begin{array}{*{20}{c}} \displaystyle{\frac{\partial^2f}{\partial x^2}} & \displaystyle{\frac{\partial^2f}{\partial x \partial y}}\\ \displaystyle{\frac{\partial^2f}{\partial y \partial x}} &\displaystyle{\frac{\partial^2f}{\partial y^2}} \end{array}} \right)\)
La notation de Monge donne à \(H\) un air moins barbare : \(H = \left( {\begin{array}{*{20}{c}} r&s\\ s&t \end{array}} \right)\)
Trois techniques permettent de faire émerger la nature des points critiques : l’étude de la convexité, les valeurs propres de la matrice hessienne (décrite en page d'optimum et valeurs propres) et le signe de la forme quadratique associée à cette dernière. Dans l’exemple ci-dessous, c’est l’étude de la convexité qui est conduite. La procédure est la suivante :
Après avoir trouvé les points candidats à l'aide d'un système de deux équations à deux inconnues, on présente la matrice hessienne en ces points. Il faut ensuite calculer son déterminant.
Si celui-ci est strictement négatif, auquel cas le signe de \(r\) est généralement différent du signe de \(t,\) le point candidat est un point selle. S’il est positif, ce point est un extremum et s’il est nul, on ne peut pas conclure et on se tourne vers une autre technique (si dans son ensemble la fonction est strictement convexe ou concave, on sait toutefois qu’il s’agit bien d’un extremum).
Lorsque le point est un extremum, on s’intéresse à \(r\) pour en savoir davantage. S’il est positif, il s’agit d’un minimum. S’il est négatif, c'est un maximum.
Note : il est fréquent de trouver dans les ouvrages des formules qui utilisent l’opposé du déterminant, c’est-à-dire \(s^2 - rt,\) avec évidemment des sens d’inégalité contraires.

Exemple
Trouver, s’il existe, le minimum de \(f(x , y)\) \(=\) \(x^2 - xy + y^2 + 2x - y + 1\)
La première étape consiste à annuler les deux dérivées partielles afin de détecter le ou les points candidats.
\(\left\{ {\begin{array}{*{20}{c}} {\displaystyle{\frac{\partial f}{\partial x}} = 2x - y + 2 = 0}\\ {\displaystyle{\frac{\partial f}{\partial y}} = -x + 2y - 1 = 0} \end{array}} \right.\)
Résolvons ce banal système d'équations. Les solutions sont \(x = -1\) et \(y = 0.\) Donc, un point unique est à considérer.
Le point \((-1 \,;0)\) est peut-être un minimum... Vérifions-le.
\(H = \left( {\begin{array}{*{20}{c}} 2&-1\\ -1&2 \end{array}} \right)\)
Le déterminant est égal à \(4 - 1 = 3\) donc \(> 0\) et \(r > 0.\) La fonction est convexe et le point de coordonnées \((-1 \,; 0)\) est bien un minimum.
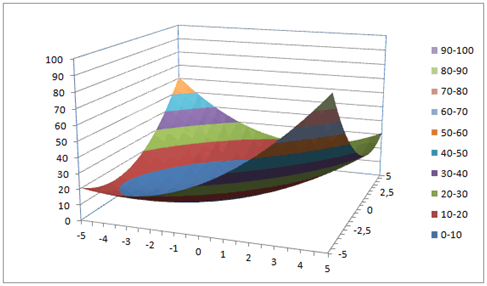
En remplaçant \(x\) et \(y\) par ces coordonnées, on constate que la valeur minimale est 0. Excel permet de visualiser la surface représentative de \(f.\) Il est difficile de déterminer graphiquement le minimum avec cette illustration mais on peut au moins constater la convexité…