Séries à termes positifs et théorèmes de comparaisons
Dans le vaste monde des mathématiques se trouve un pays particulièrement étendu et il s’agit de celui des séries. Souvent, ces séries sont à termes positifs, c’est-à-dire qu’elles sont composées de sommes partielles de suites dont les éléments sont tous positifs ou nuls. Les suites de sommes partielles sont donc croissantes puisqu’on leur ajoute un élément positif chaque fois qu’elles sont incrémentées de 1.
Maths appliquées
Certaines séries observées, par exemple sur des phénomènes économiques, peuvent faire l'objet de tests de convergence bien pratiques (précisons que seules les séries convergentes sont vraiment intéressantes).
Par ailleurs, si les termes sont toujours négatifs, il est facile de retomber sur une série à termes positifs.

Attention, une série peut n’être positive qu’à partir d’un certain rang.
Point fondamental : une série à termes positifs converge si la suite des sommes partielles est majorée.
Illustration simple
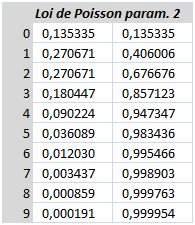
Ci-dessous, le tableau indique les premières valeurs prises par une loi de probabilité : la loi de Poisson de paramètre 2 pour \(k = 0, 1, 2...\) Ainsi ces valeurs, positives et inférieures à 1 puisque ce sont des probabilités, sont-elles celles d'une suite. La dernière colonne est celle des probabilités cumulées, donc d'une série. À l'infini, elle converge évidemment vers 1.
Comparaisons
Critère de comparaison : c’est le même type d’astuce qui est employé par les théorèmes sur les limites de fonctions et limites de suites. Si, pour un rang \(n,\) \(Su_n\) est inférieur à \(Sv_n\) et que l’on sait pertinemment que \(Sv_n\) converge, alors il est bien évident que \(Su_n\) converge aussi. Inversement, si l’on sait que \(Su_n\) diverge, alors \(Sv_n\) diverge aussi.
Prenons l’exemple assez facile de la série suivante :
\(\displaystyle{\sum\limits_{n \ge 1} {\frac{1}{{n(n + 1)}}}}\)
Comment savoir si elle converge ? En la comparant à une série de Riemann \(\sum {\frac{1}{{{n^\alpha }}}} \) (voir la page sur les séries). Les termes \(n\) étant des naturels, on sait que \(n(n + 1)\) est fort logiquement supérieur à \(n^2.\) Donc, l’inverse, qui n’est autre que \(\frac{1}{n(n+1)},\) est quant à lui inférieur à \(\frac{1}{n^2}.\) Or, on sait que la série de Riemann est convergente. Par conséquent, notre série (qui lui est inférieure pour un rang donné) converge elle aussi…
La comparaison logarithmique : c’est une « extension » du critère précédent. Cette fois, c’est \(\frac{u_{n+1}}{u_n}\) qui est inférieur, pour tout \(n,\) à \(\frac{v_{n+1}}{v_n}.\) Mais on retrouve les mêmes cas de figure : si \(Sv_n\) converge, \(Su_n\) en fait de même et si cette dernière diverge, alors \(Sv_n\) aussi.
La comparaison à une intégrale : comme on le constate, l’expression des séries se présente sous une forme \(Sf(n).\) Si la fonction \(f\) est positive, continue et décroissante, alors son intégrale et la série sont de même nature.
Opérations
Si la suite \(\frac{u_n}{v_n}\) admet une limite finie différente de zéro, ça signifie que les séries \(Su_n\) et \(Sv_n\) sont de même nature (soit convergentes, soit divergentes).
Par ailleurs, la nature d’une série ainsi que sa somme (si elle est finie) ne sont pas affectées si des termes sont permutés (commutativité) ou s’ils sont regroupés d’une façon ou d’une autre (associativité).
Applications
Une application simple se trouve en page de modèle de Gordon-Shapiro.
Bibliographie (épuisée) : les Séries mathématiques, Gaston Casanova, Que sais-je? (n° 1567), 1981. Analyse II Mathématiques pour les sciences économiques, exercices corrigés, Lecoutre et Pilibossian, Dunod 1998.
