Intégrales et exemples simples
Si vous êtes en terminale générale, vous pouvez mesurer votre chance : cette page a été rédigée pour vous. Dans votre programme officiel de maths, il est précisé que vous devez aborder le chapitre sur l’intégration par le biais de figures géométriques vues au collège. Alors voilà, l’histoire commence ainsi…
Intégrale d’une fonction continue positive
En premier lieu, définissons.
Soit un repère orthogonal du plan et les points de coordonnées \(I(1\,;0),\) \(J(0\,;1)\) et \(K(1\,;1).\)
Une unité d’aire est l’aire du rectangle \(OJKI.\) On l’écrit souvent en abrégé : u.a.
À présent, soit \(a\) et \(b\) deux réels, \(f\) une fonction continue positive sur l’intervalle \([a\,;b]\) et \({\mathscr{C}_f}\) sa courbe représentative.
L’intégrale de \(f\) entre \(a\) et \(b\) est le domaine, en u.a., délimité par l’axe des abscisses, par \({\mathscr{C}_f}\) et par les droites d’équations \(x = a\) et \(x = b\) (\(a\) et \(b\) sont les bornes de l’intégrale). On la note avec ce symbole créé par l'un des découvreurs du calcul intégral, Gottfried Wilhelm Leibniz :
\[\int_a^b {f(x)dx} \]
Voici un exemple d'aire, comprise entre \(a = -3\) et \(b = 0,\) l'axe des abscisses et une courbe représentative d'une fonction.
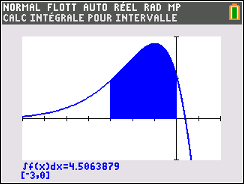
La lecture graphique de l'aire étant très approximative, voyons comment la déterminer par le calcul.
Théorème et propriétés
Théorème : soit la fonction \(F\) définie sur [a ; b] par :
\[F(x) = \int_a^x {f(t)dt} \]
Si \(f\) est continue et positive sur \([a\,;b],\) \(F\) est dérivable sur \([a\,;b]\) et a pour dérivée \(f.\)
\(F\) est une primitive de \(f.\) En l'occurrence, c'est son unique primitive telle que \(F(a) = 0.\)
Le théorème fondamental du calcul intégral :
\[\int_a^b {f(t)dt} = F(b) - F(a)\]
Le calcul intégral repose sur plusieurs propriétés : linéarité, positivité, relation de Chasles, ordre... (seule la relation de Chasles est expressément mentionnée dans le programme de maths complémentaires).
Linéarité (avec \(m\) et \(k\) réels) :
\(\int_a^b {\left[ {kf(x) + mg(x)} \right]dx}\) \(=\) \( k\int_a^b {f(x)dx} + m \int_a^b {g(x)dx} \)
Relation de Chasles (avec \(b \in [a\,;c]\)) :
\(\int_a^b {f(x)dx} + \int_b^c {f(x)dx} = \int_a^c {f(x)dx} \)
Ordre : si pour tout \(x \in [a\,; b],\) \(f(x) \leqslant g(x)\) alors...
\(\int_a^b {f(x)dx} \leqslant \int_a^b {g(x)dx} \)
Exemple 1 : fonction constante
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = 2,\) représentée par la courbe \({\mathscr{C}_f}\) dans un repère orthogonal (\({\mathscr{C}_f}\) prend donc la forme d’une droite horizontale). Calculons l’aire comprise entre l’axe des abscisses, \({\mathscr{C}_f}\) et les droites d’équations \(x = -1\) et \(x = 3.\)
Technique 1 : nous avons compris que l’aire a la forme d’un rectangle, de hauteur 2 et de longueur 4. Par conséquent, l’intégrale est égale à 8 u.a. Vérification :
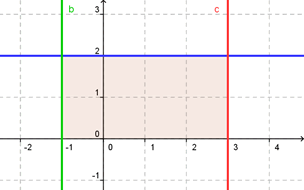
Nous comptons bien huit carreaux qui correspondent chacun à une u.a.
Technique 2 : une fonction dont la dérivée est \(f(x) = 2\) est \(F(x) = 2x.\)
Calculons \(F(3) – F(-1)\) \(=\) \((2 × 3) - [2 × (-1)]\) \(=\) \(6 + 2 = 8.\)
Exemple 2 : fonction linéaire
Soit la fonction linéaire \(g\) définie sur \(\mathbb{R}\) par \(g(x) = 3x,\) représentée dans le plan par la courbe \({\mathscr{C}_g}.\)
Déterminons l’aire comprise entre l’axe des abscisses, \({\mathscr{C}_g}\) et les droites d’équations \(x = 1\) et \(x = 2.\)
Voyons à quoi l’aire peut bien ressembler…
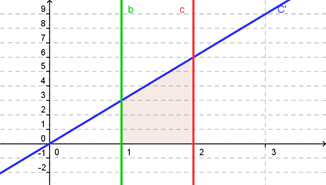
Eh oui, à un trapèze rectangle !
Technique 1 : nous constatons que l’aire peut être décomposée entre un rectangle surmonté d’un triangle rectangle. L’aire du rectangle est de 3 et celle du triangle rectangle est de la moitié de 3, soit 1,5. Par conséquent, l’aire est égale à 4,5 u.a.
Technique 2 : elle commence par le plus difficile, c’est-à-dire trouver une fonction \(G\) telle que \(G’(x) = 3x.\) Mais ne zappez pas cette technique car c’est elle qu’il vous faudra utiliser par la suite ! (ne vous inquiétez pas, vous apprendrez des astuces pour « dériver à l’envers »).
Nous trouvons \(G(x) = \frac{3}{2}x^2\)
Amusez-vous à dériver \(G,\) juste pour vérifier…
Ainsi :
\(\int_1^2 {g(x)dx} = G(2) - G(1)\)
\(= \frac{3}{2}2^2 - \frac{3}{2}1^2\) \(=\) \(\frac{12}{2} - \frac{3}{2} = 4,5\)
Magie des mathématiques ! Nous trouvons le même résultat !
Observations
Vous remarquerez que nous aurions pu intégrer une fonction affine, les choses n’auraient pas été plus compliquées.
Vous remarquerez également que ces deux exemples permettaient de choisir entre deux techniques. Mais lorsqu’il s’agira de déterminer une aire lorsque la courbe représentative de la fonction à intégrer n’est pas droite, alors seules les techniques 2 seront utilisables ! (que l’avenir est angoissant !)
