Démonstrations de valeurs trigonométriques
Dans le programme de trigonométrie de première générale, vous ne trouverez pas moins de trois démonstrations à ingurgiter. Si ça vous paraît trop copieux pour être digéré, cette page devrait avoir l’effet d’une tisane bienfaisante…
\(\cos(\frac{\pi}{4})\)
Nous allons montrer de deux façons que \(\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\)
D’abord, de façon géométrique.
Partons d’un carré de côté 1. Selon le théorème de Pythagore, la diagonale mesure \(\sqrt{2}.\) En effet, le carré forme deux triangles rectangles isocèles et sa diagonale est leur hypoténuse. Donc sa mesure est la racine carrée de \(1^2 + 1^2.\)
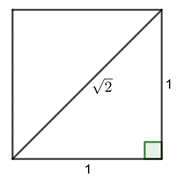
L’angle formé par cette diagonale est de 45°. Si vous connaissez le cercle trigonométrique, vous savez que cela correspond à \(\frac{\pi}{4}\) radians.
Cela étant rappelé, à quoi peut bien être égal à \(\cos\left(\frac{\pi}{4}\right)\) ? Vous vous souvenez bien sûr de la formule du cosinus :
\[{\rm{cosinus = }}\frac{{{\rm{côté\; adjacent}}}}{{{\rm{hypoténuse}}}}\]
Donc, \(\cos\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}.\) Comme on évite de laisser un radical au dénominateur, écrivons \(\frac{1}{\sqrt{2}}\) \(= \frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\) \(= \frac{\sqrt{2}}{2}.\)
Remarquez que \(\sin\left(\frac{\pi}{4}\right)\) est aussi égal à \(\frac{\sqrt{2}}{2}.\)
Autre démonstration : on utilise la formule \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) vue en seconde.
Donc, cas particulier : \({\cos ^2}\left(\frac{\pi}{4}\right) + {\sin ^2}\left(\frac{\pi}{4}\right) = 1.\)
On sait que \(\sin\left(\frac{\pi}{4}\right) = \cos\left(\frac{\pi}{4}\right)\) (voir le carré ci-dessus).
Donc \(2\cos^2\left(\frac{\pi}{4}\right) = 1\)
\(\Leftrightarrow \cos^2\left(\frac{\pi}{4}\right) = \frac{1}{2}\)
\(\Leftrightarrow \cos^2\left(\frac{\pi}{4}\right) - \frac{1}{2} = 0\)
Factorisons (identité remarquable)
\(\left(\cos\left(\frac{\pi}{4}\right) + \sqrt{\frac{1}{2}}\right) \left(\cos\left(\frac{\pi}{4}\right) - \sqrt{\frac{1}{2}}\right) = 0\)
Un produit est nul si l’un de ses facteurs est nul.
\(\left(\cos\left(\frac{\pi}{4}\right) + \sqrt{\frac{1}{2}}\right) = 0\) ou \(\left(\cos\left(\frac{\pi}{4}\right) - \sqrt{\frac{1}{2}}\right) = 0\)
\(\Leftrightarrow\cos\left(\frac{\pi}{4}\right) = -\sqrt{\frac{1}{2}}\) ou \(\cos\left(\frac{\pi}{4}\right) = \sqrt{\frac{1}{2}}\)
Comme \(\frac{\pi}{4} \in [0\,; \frac{\pi}{2}],\) on sait que son cosinus est positif (Cf. le cercle) donc la seconde solution ne convient pas.
Par propriété, \(\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}\)
Comme nous avons vu plus haut que \(\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\) nous avons démontré que \(\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) (youpi).
\(\cos(\frac{\pi}{3})\)
Montrons à présent que \(\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}.\) L’approche sera différente des deux démonstrations précédentes.
Rappelons que l’angle plat est égal à \(\pi\) (soit 180°). Vous avez appris au collège que la somme des angles d’un triangle vaut 180°. Chaque angle d’un triangle équilatéral est donc égal à \(\frac{\pi}{3}\) radians.
Nous cherchons donc le cosinus d’un angle de triangle équilatéral.
Soit un triangle équilatéral \(ABC\) de côté 1 et soit \(D\) le pied de la médiane issue de \(C\) (la médiane étant aussi la hauteur puisque le triangle est équilatéral).
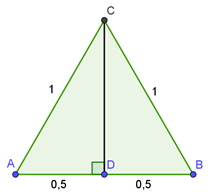
Si \(AC\) est le rayon du cercle trigonométrique de centre \(A,\) alors \(B\) appartient au cercle. La figure ci-dessous montre bien que le cosinus de \(\frac{\pi}{3}\) est \(\frac{1}{2}.\)
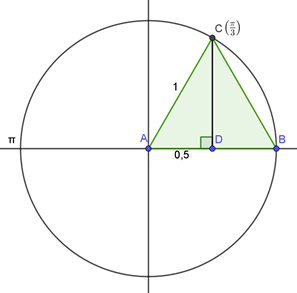
\(\sin(\frac{\pi}{3})\)
Et le sinus dans tout çà ?
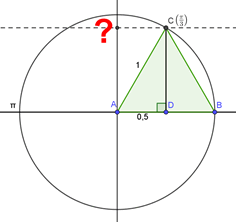
On peut là encore le trouver de plusieurs façons : côté opposé sur hypoténuse, formule vue en seconde… Mais après tout, pourquoi pas ce bon vieux théorème de Pythagore ? Le triangle \(ACD\) est rectangle en \(D.\) Or, nous savons que \(AC = 1\) et \(AD = 0,5.\) Nous cherchons \(CD.\)
\(CD^2 = 1^2 - 0,5^2\)
\(\Leftrightarrow CD^2 = 0,75 = \frac{3}{4}\)
Donc \(CD = \sqrt{\frac{3}{4}}\) (et pas \(-\sqrt{\frac{3}{4}}\) puisqu’une distance est positive).
Soit \(CD = \frac{\sqrt{3}}{2}.\) Ainsi, \(\sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}.\)
