Exercice avec dérivée de fonction trigonométrique
Le trapèze est un quadrilatère qui a inspiré quantité d’artistes (ci-dessous, le manteau trapèze de Carven, fin des années 50, musée de la Mode de la Ville de Paris). Et vous, vous inspire-t-il ? Si oui, voici un petit exercice de niveau terminale, maths de spécialité.

Énoncé
On considère le trapèze isocèle \(ABCD\) tel que \(AB = BC = CD = 1.\)
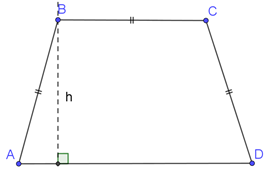
Soit \(x\) la mesure de l’angle \(Â\) (en radians).
Votre mission consiste à déterminer \(x\) pour que l’aire du trapèze soit maximale.
- Déterminer l’intervalle des valeurs possibles de \(x.\)
- Exprimer la hauteur \(h\) en fonction de \(x.\)
- Soit \(\mathscr{A}\) l’aire du trapèze. Déterminer une expression de la fonction \(\mathscr{A}.\) Rappelons que si un trapèze a pour petite base \(b\) et pour grande base \(B\) son aire est \(\mathscr{A} = \frac{B + b}{2} × h.\)
- Tracer le tableau de variation de \(\mathscr{A}\) sur son ensemble de définition. Pour cela, vous devrez déterminer que la dérivée peut s’écrire \(\mathscr{A}(x)’ = 2 \cos^2 x + \cos x - 1\) puis procéder à un changement de variable.
En déduire l’aire maximale du trapèze.
Corrigé
1- Le cercle trigonométrique n’ayant aucun secret pour vous, vous en avez conclu que les valeurs possibles de \(x\) appartiennent à l’intervalle \(]0\, ;\frac{π}{2}].\) Nous avons exclu 0 pour que le trapèze ne ressemble pas à une droite mais ce détail n’est pas d’une grande importance.
2- Cette question peut être résolue dès le collège. La hauteur issue de \(B\) permet de tracer un triangle rectangle dont l’hypoténuse est \(AB\) c’est-à-dire 1.
Comme \(h\) est le côté opposé à \(A\) et que nous connaissons l’hypoténuse, c’est le sinus qu’il faut sortir de sa boîte à outils.
\(\sin x = \frac{h}{AB} = h\)
3- Soit \(H\) le pied de la hauteur issue de \(B\) \(H ∈ [AD].\)
Nous devons trouver \(AH.\)
D’après le théorème de Pythagore, \(AB^2 = h^2 + AH^2\)
Donc \(AH^2 = 1 - h^2\)
\(⇔ AH^2 = 1 - \sin^2 x\)
Vous connaissez la formule fondamentale de la trigonométrie : \(\sin^2 x + \cos^2 x = 1\)
D’où \(AH^2 = \cos^2 x\)
\(⇔ AH = \sqrt{\cos^2 x}\) ou \(AH = -\sqrt{\cos^2 x}\) mais cette deuxième solution, négative, ne peut être retenue puisque \(AH\) est une longueur.
Nous pouvons donc affirmer que \(AH = \cos x.\)
Nous avons obtenu \(h = \sin x,\) \(BC = 1\) et \(AD = 1 + 2 \cos x.\)
Donc \(\mathscr{A}(x) = \frac{h(1 + 1 + 2 \cos x)}{2} × \sin x\) \(=\) \(\sin x (\cos x + 1)\)
Il était possible d’arriver au même résultat sans connaître la formule de l’aire d’un trapèze (somme des aires d’un rectangle et de deux triangles rectangles), les calculs n’étant pas non plus très longs.
4- Pour tracer le tableau de variation de cette fonction, nous devons établir sa dérivée puis étudier son signe.
Il s’agit d’une fonction produit. Rappel de la formule : \((u(x)v(x))’ = u’(x)v(x) + u(x)v’(x)\) avec \(u(x) = \sin x\) et donc \(u’(x) = \cos x,\) \(v(x) = \cos x + 1\) et \(v’(x) = - \sin x\) (voir les dérivées de fonctions trigonométriques).
\(\mathscr{A}’(x) = \cos x (\cos x + 1) - \sin x \sin x\)
\(⇔ \mathscr{A}’(x) = \cos^2 x + \cos x - \sin^2 x\)
\(⇔ \mathscr{A}’(x) = \cos^2 x + \cos^2 x - (1 - \cos^2 x)\)
\(⇔ \mathscr{A}’(x) = \cos^2 x + \cos x - 1 + \cos^2 x\)
\(⇔ \mathscr{A}’(x) = 2 \cos^2 x + \cos x - 1\)
Soit \(X = \cos x.\) Donc \(X ∈ [0\, ;1[.\)
\(\mathscr{A}’(X) = 2 X^2 + X - 1\)
Posons l’inéquation \( 2 X^2 + X - 1 = 0\)
Le discriminant vaut \(1^2 - 4 × 2 × (-1) = 9.\) Il est positif. Le trinôme admet deux racines.
Soit \(X_1 = \frac{-1 - \sqrt{9}}{2 \times 2} = -1\) et \(X_2 = \frac{-1 + \sqrt{9}}{2 \times 2} = \frac{1}{2}.\) Comme 1 est en-dehors de notre intervalle, le tableau de signes du trinôme ressemble à ceci :
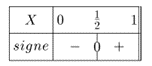
Donc \(\cos x = \frac{1}{2}\) et par conséquent \(x = \frac{π}{3}.\)
\(\mathscr{A}(\frac{π}{3}) = (\frac{1}{2} + 1) × \frac{\sqrt{3}}{2}\) \(=\) \(\frac{3 \sqrt{3}}{4}\)
Attention, sur l’intervalle de \(x\) que nous étudions, la fonction cosinus est décroissante. Donc il faut inverser les signes du tableau précédent lorsqu’on revient à notre variable initiale \(x.\)
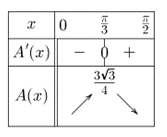
L’aire maximale vaut \(\frac{3 \sqrt{3}}{4}\) soit environ 1,299.
