Produit scalaire et orthogonalité en géométrie analytique
Voici deux exercices sur l’orthogonalité dans un plan muni d’un repère orthonormé. Ils font intervenir les produits scalaires. Leur niveau de difficulté est celui d’une première générale (hors repère orthonormé, voir l'exercice produit scalaire en géométrie). D'autres exercices figurent en page de vecteur normal à une droite.
Rappels
1- Un vecteur directeur à la droite d’équation cartésienne \(\alpha x + \beta y + \delta = 0\) est : \(\overrightarrow u \left( {\begin{array}{*{20}{c}} { - \beta }\\ \alpha \end{array}} \right)\)
2- Soit les vecteurs \(\overrightarrow u \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right)\) et \(\overrightarrow v \left( {\begin{array}{*{20}{c}} x'\\ y' \end{array}} \right)\)
L’expression analytique de leur produit scalaire dans un repère orthonormé est \(xx’ + yy’.\)
3- Par ailleurs, deux vecteurs sont orthogonaux lorsque leur produit scalaire est nul.
Exercice 1
Soit un plan muni d’un repère orthonormé \(( {O\,;\overrightarrow i \,;\overrightarrow j } )\) et soit les points de ce plan \(A(0\,;5)\), \(B(4\,;-1)\), \(C(1\,;2)\), \(D(4\,;1)\) et \(E(m\,;6).\) Soit \(F\) le point d’intersection des droites \((AB)\) et \((CD).\)
Trouver les coordonnées de \(E\) de façon que les droites \((FE)\) et \((CD)\) soient perpendiculaires.
Exercice 2
Soit \((D)\) la droite d’équation réduite \(y = 2x - 1\) dans un repère orthonormé. Déterminer une équation de la droite \((D’)\) perpendiculaire à \((D)\) qui passe par le point \(A(1\,;6).\)

Corrigé 1 (détaillé)
Déterminons en premier lieu les équations cartésiennes des droites \((AB)\) et \((CD)\) afin de trouver les coordonnées de \(F.\)
Pour cela il faut connaître l'expression des vecteurs \(\overrightarrow {AB} \) et \(\overrightarrow {CD} \) (on pourrait également employer les équations réduites des droites).
\(\overrightarrow {AB} \left( {\begin{array}{*{20}{c}} {4 - 0}\\ { - 1 - 5} \end{array}} \right)\), soit \(\overrightarrow {AB} \left( {\begin{array}{*{20}{c}} 4\\ { - 6} \end{array}} \right)\) et \(\overrightarrow {CD} \left( {\begin{array}{*{20}{c}} {4 - 1}\\ {1 - 2} \end{array}} \right)\), soit \(\overrightarrow {CD} \left( {\begin{array}{*{20}{c}} 3\\ { - 1} \end{array}} \right)\)
D’où \((AB)\) a pour équation \(-6x - 4y + \delta = 0.\)
Afin de trouver \(\delta\), remplaçons \(x\) et \(y\) par les coordonnées de \(A\), soit \(-20 + \delta = 0.\) Il vient \(\delta =20.\)
Donc \((AB)\) a pour équation \(-6x - 4y + 20 = 0\) ou, si l’on divise les deux membres par 2, \(-3x - 2y + 10 = 0.\)
De même, on trouve une équation pour \((CD)\) : \(x + 3y - 7 = 0.\)
Les coordonnées du point d’intersection se calculent grâce à un système de deux équations.
\(\left\{ {\begin{array}{*{20}{c}} { - 3x - 2y = - 10}\\ {x + 3y = 7} \end{array}} \right.\)
Utilisons la technique de la substitution.
\( \left\{ {\begin{array}{*{20}{c}} { - 3( - 3y + 7) - 2y = - 10}\\ {x = - 3y + 7} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = \frac{{11}}{7}}\\ {x = \frac{{16}}{7}} \end{array}} \right.\)
Donc \(F\left( {\frac{{16}}{7};\frac{{11}}{7}} \right)\)
Déterminons à présent le vecteur \(\overrightarrow {FE}. \)
\(\overrightarrow {FE} \left( {\begin{array}{*{20}{c}} {m - \frac{{16}}{7}}\\ {6 - \frac{{11}}{7}} \end{array}} \right)\), soit \(\overrightarrow {FE} \left( {\begin{array}{*{20}{c}} {m - \frac{{16}}{7}}\\ {\frac{{31}}{7}} \end{array}} \right)\)
C’est ici qu’intervient (enfin !) le produit scalaire.
\(\overrightarrow {CD} .\overrightarrow {FE} = 3\left( {m - \frac{{16}}{7}} \right) - \frac{{31}}{7}\)
Les vecteurs sont orthogonaux (donc les droites qui les supportent sont perpendiculaires) si et seulement si leur produit scalaire est nul.
\(3m - \frac{{79}}{7} = 0 \Leftrightarrow m = \frac{{79}}{{21}}\)
Par conséquent, \(E\left( {\frac{{79}}{{21}}\,;6} \right).\)
GeoGebra nous offre une vue imprenable sur cet exercice :
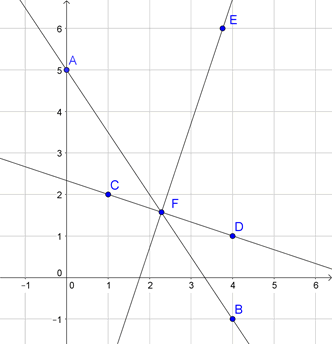
Corrigé 2
Première étape : une équation cartésienne de \((D)\) est \(-2x + y + 1 = 0.\) Un vecteur directeur de \((D)\) a donc pour coordonnées \((-1\,;-2).\)
Deuxième étape : il faut exprimer les coordonnées d’un vecteur quelconque passant par \(A.\)
Soit le point \(M(x\,;y).\) Nous obtenons \(\overrightarrow {AM} \left( {\begin{array}{*{20}{c}} {x - 1}\\ {y - 6} \end{array}} \right)\)
Troisième étape : utiliser la formule du produit scalaire \((xx'- yy').\) Cette expression est valide puisque le repère est orthonormé. L’expression doit être égale à 0 pour qu’il y ait orthogonalité.
\((-x - 1) -2(y - 6) = 0\)
\( \Leftrightarrow - x - 2y + 13 = 0\) ou, si l’on préfère l’équation réduite, \(y = -0,5x + 6,5.\)
