Fonctions sécante et autres trigonométriques
Il existe quelques fonctions trigonométriques qui, sans faire expressément partie du programme de terminale, apparaissent quelquefois au détour d’un exercice. Elles sont présentées ici...
La fonction sécante
C’est l’inverse de la fonction cosinus. \(\sec x = \frac{1}{\cos x}\)
Ensemble de définition : dans la mesure où les cosinus de \(\frac{\pi}{2}\) et de \(-\frac{\pi}{2}\) modulo \(2 \pi\) ne valent rien (nous voulons dire qu'ils sont nuls), la fonction sécante n’est pas définie pour ces valeurs. Périodicité : la période s’établit à \(2 \pi.\) Parité : la fonction est paire puisque \(\cos -x = \cos x.\)
La fonction cosécante est l’inverse de la fonction sinus. Elle a la même périodicité mais elle est impaire puisque c’est une simple translation de la précédente :
\(\csc x = \frac{1}{\sin x} = \sec(x - \frac{\pi}{2})\)
C’est d’ailleurs très simple à démontrer avec les formules de trigonométrie :
\(\cos (\frac{\pi}{2} - x) = \sin x\) et \(\sin (\frac{\pi}{2} - x) = \cos x\)
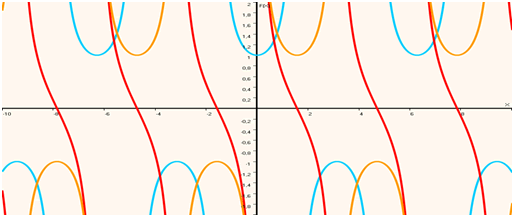
On en déduit que la fonction sécante admet le point de coordonnées \((\pi\,; 0)\) comme centre de symétrie et que la fonction cosécante admet la droite d’équation \(x = \frac{\pi}{2}\) comme axe de symétrie.
La fonction cotangente étant l’inverse de la fonction tangente, \(\cot x = \frac{\cos x}{\sin x}\)
Ci-dessus figurent les courbes représentatives des fonctions sécante (en bleu), cosécante (en orange) et cotangente (en rouge). Réalisation avec Sine qua non.
Note : voir en page de trigonométrie les liens qui existent entre le triangle rectangle et les fonctions sécante, cosécante et cotangente.
La fonction « dos de chameau »
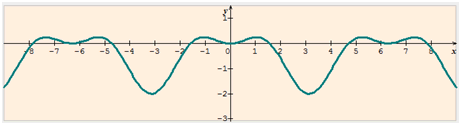
S’il n’existe pas de fonction « trompe d’éléphant », « cou de girafe » ou « nageoire de requin-marteau », il en existe bien une dont la courbe représentative montre une double bosse qui réapparaît périodiquement et peut faire penser, avec un peu d'imagination, à une caravane de chameaux. Soit la fonction \(f\) définie par \(f(x) = \cos x - \cos^2 x.\)
Définie sur \(\mathbb{R}\), elle est paire et périodique.
Pour quelles valeurs admet-elle des extremums entre \(- \pi\) et \(\pi\) ?
Sa dérivée est \(f’(x) = \sin x (-1 + 2 \cos x).\) Elle s’annule lorsque \(\sin x = 0,\) c’est-à-dire en 0 et en \(\pi,\) et lorsque \(\cos x = \frac{1}{2},\) c’est-à-dire en \(-\frac{\pi}{3}\) et en \(\frac{\pi}{3}.\) Il s’ensuit qu’elle est minorée et majorée, respectivement par -2 et par 0,25.
Une fonction en « papillon »
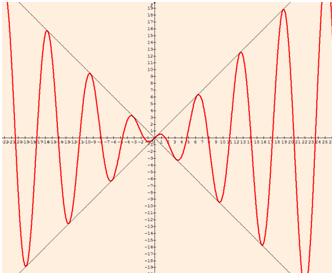
Restons dans le bestiaire mathématique. Là aussi, il s’agit d’un type de fonction davantage rencontrée en physique qu’en économie : \(f(x) = x \cos x.\)
On montre facilement qu’elle est impaire mais elle n’est pas périodique. Sa courbe représentative oscille entre les droites \((D)\) et \((D’)\) d’équations respectives \(y = x\) et \(y = -x\) pour la bonne raison que \(\cos x\) oscille entre -1 et 1. Les points de tangence entre la courbe représentative de \(f\) et \((D)\) se situent là où \(\cos x = 1,\) c’est-à-dire en 0 et \(2kπ\) (pour tout \(k\) entier relatif). Les points de tangence entre la courbe et \((D’)\) se situent là où \(\cos x = -1,\) donc en \(π\) modulo \(2π.\)
Vous connaissez la formule de dérivée d'une fonction produit et admettrez volontiers que \(f'(x) = \cos x - x \sin x.\) Ainsi \(f’(0) = 1\) et \((D)\) est une tangente qui traverse la courbe sur l’origine du repère.
Enfin, une dernière grande classique…
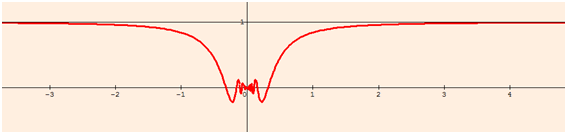
Pour finir en beauté, voici \(f(x) = x \sin \frac{1}{x}.\) Déterminons les limites de cette fonction paire, en zéro et à l’infini.
Un corollaire du théorème des gendarmes est que le produit entre une fonction de limite nulle et une fonction bornée tend vers zéro. Donc…
\(\mathop {\lim }\limits_{x \to 0} x\sin \frac{1}{x} = 0\)
Quelle est la limite à l’infini ? Nous utiliserons cette fois-ci les fonctions équivalentes (pas au programme de terminale). Il est de notoriété publique qu’en zéro, les fonctions \(f:x \mapsto x\) et \(g: x \mapsto \sin x\) sont équivalentes. Par conséquent, si l’on procède à un changement de variable, on s’aperçoit qu’à l’infini \(\sin \frac{1}{x}\sim \frac{1}{x}\)
Donc la limite est égale à 1. La preuve (qui mathématiquement n'est pas une preuve) en image :